例1 用逐次逼近法求初值问题
在初始区域
，使误差不超过0.25的近似解．
解 该方程是非线性一阶微分方程．根据误差估计式(2)要确定在误差范围内的
来，即要求出估计式(2)中的
和
．
取区域
由于
在区域
上
故
因此解的存在区间是
由于
故李普希兹常数
由误差估计式（2）
取
时即可．因为时，
第二次近似解就满足误差要求．取
在要求的误差范围内的近似解为
例2 初值问题
证明 在
内，其解可用逐次逼近法，并求三次近似解．
解 该微分方程组是非线性的一阶微方程组，因为它含有未知函数
的平方项．取
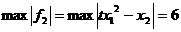
在所给区域上取
，因为此时
故
故用逐次逼近法其解存在区间为
.
求第三次近似解
取
时，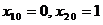
,于是一阶微分方程组的等价积分方程组为
例3 判断方程奇点的类型
解 因为
的系数的行列式
有唯一的
．即（16）有唯一的奇点（0,0）．
将（16）化成约当型．先求特征根得
其次求
，
的特征向量满足方程：
取
，则
．故
特征向量为
．对应的特征向量满足方程：
取
则
．故
的特征向量为
.
由于两特征向量线性无关，故矩阵
为
由求逆矩阵的方法可知
为
故
由于
，故
；
由于
，所以
即
在
平面上有奇点（o、o），由于特征根
是不等的负实根，故在平面上有奇点（o、o）是稳定的结点．
由于即
即
因此平面上坐标轴
，变到
平面上为两条直线：
由于方程组（10）的解为
又由于
，即
故微分方程级（9）的通解为
（11）
当
时，
，奇点
在平面上是稳定结点．
特别，当
时, 代入（11）得，
，故微分方程组（9）过点（1，2，0）的积分曲线为
消去
得在平面上的轨线
，对应于平面上的
轴．其轨线方向由微分方程组（9）右端可得，它是指向原点．
特别：当
时, 代入（11）得
，故微分方程组（9）过点（3，14，0）的积分曲线为
消去得在平面上轨线为
，对应于平面上的
轴．而轨线方向由微分方程组（9）的右端可得它是指向原点．