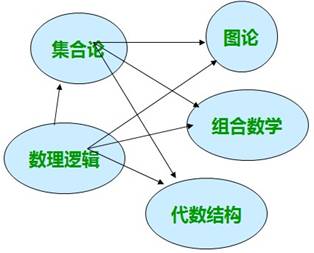
离散数学的教学内容有数理逻辑、集合论、组合数学、代数结构和图论，各部分教学内容之间的关系如下：

本课程学习课时为60课时，各部分教学内容有：

第一章命题逻辑

课时：8小时。

学习目标：掌握命题及五个命题联结词的概念，重点掌握命题公式类型的判定，熟悉常用的等价式与蕴涵式，重点掌握求主范式的方法，重点掌握利用P规则、T规则和CP规则进行命题逻辑的推理。

第一节命题与联结词

第二节命题公式、翻译与真值表

第三节公式分类与等价式

第四节对偶式与蕴涵式

第五节公式标准型-范式

第六节公式主范式

第七节命题逻辑的推理理论

第二章谓词逻辑

课时：6小时。

学习目标：掌握谓词、量词、自由变元和约束变元的概念，了解谓词公式的解释与分类，熟悉常用的谓词等价式与蕴涵式，重点掌握利用UG规则、US规则、EG规则和ES规则进行谓词逻辑的推理。

第一节基本概念

第二节谓词公式与翻译

第三节自由变元和约束变元

第四节谓词公式的解释与分类

第五节谓词演算的等价式与蕴涵式

第六节谓词演算的推理理论

第三章集合

课时：6小时。

学习目标：掌握集合的基本概念、运算及性质，掌握空集、全集和幂集的概念，重点掌握集合相等的证明，了解集合划分的概念，掌握排列、组合的概念。重点掌握容斥原理及其应用，了解抽屉原理

第一节集合的概念与表示法

第二节集合的运算与性质

第三节集合的划分与覆盖

第四节乘法原理、加法原理

第五节容斥原理和抽屉原理（鸽巢原理）

第四章关系

课时：8小时。

学习目标：掌握序偶、笛卡尔积、关系的概念，熟练掌握关系性质的判定，熟练掌握等价关系的证明，重点掌握偏序关系与哈斯图

第一节序偶与笛卡尔积

第二节关系及其表示

第三节复合关系及逆关系

第四节关系的性质

第五节关系的闭包

第六节等价关系和等价类

第七节偏序关系

第五章函数

课时：2小时。

学习目标：掌握函数的概念，重点掌握单射、满射、双射的证明，了解集合的基数、可数集、不可数集的概念，掌握基数的比较方法

第一节函数的概念

第二节逆函数和复合函数

第三节集合的基数

第六章整除

课时：4小时。

学习目标：掌握因数、倍数、素数、合数、最大公因数、最小公倍数的概念，重点掌握带余除法与辗转相除法，求最大公因数和最小公倍数，了解算术基本定理

第一节因数和倍数

第二节素数和合数

第三节带余除法与辗转相除法

第四节最大公因数和最小公倍数

第五节算术基本定理

第七章同余，属于自学内容。

第八章代数结构

课时：10小时。

学习目标：掌握代数系统的概念，重点掌握群、子群、正规子群的证明方法，掌握群同态和群同构的证明，掌握循环群的概念，重点掌握循环群相关结论的证明

第一节代数系统的定义

第二节代数系统的性质

第三节半群和独异点

第四节群与子群

第五节循环群

第六节群的同态与同构

第九章格与布尔代数

课时：6小时。

学习目标：掌握格、分配格、有界格、有补格、有补分配格和布尔代数的概念，能够判别某个偏序集或代数系统是否构成格

第一节格的定义与性质

第二节特殊格

第三节布尔代数

第十章图

课时：10小时。

学习目标：掌握图的基本概念，理解路、回路与连通性的概念，掌握图的邻接矩阵，掌握欧拉图和哈密顿图的判定，了解二部图及匹配的概念，了解平面图的概念，重点掌握欧拉公式及相关结论的证明，掌握无向树和根树的概念，重点掌握求最小生成树和最优二叉树的方法，掌握求最短路径的方法

第一节图的基本概念

第二节路、回路与连通性

第三节图的矩阵表示

第四节欧拉图和哈密顿图

第五节二部图与匹配

第六节平面图

第七节树及其应用

第八节最短路径